1. Metoda geometrii inwersyjnej

Umieszczamy w dowolnym punkcie pustyni klatkę, wchodzimy do niej i zamykamy się od wewnątrz. Przeprowadzamy operację inwersji przestrzeni względem klatki. Teraz lew jest wewnątrz klatki, my zaś na zewnątrz.

2. Metoda geometrii rzutowej

Bez ograniczenia ogólności rozumowania możemy Saharę traktować jako płaszczyznę. Rzutujemy ją na prostą, tę zaś na punkt znajdujący się wewnątrz klatki. Kłopot z głowy.

3. Metoda Bolzano-Weierstrassa

Przecinamy pustynię linią prostą z północy na południe. Lew znajduje się teraz w jej wschodniej lub zachodniej części. Przecinamy więc tę część prostą idącą z zachodu na wschód. Æwiartkę pustyni, w której teraz znajdzie się lew, przecinamy linią północ-południe.

Kontynuujemy ten proces do nieskończoności, wznosząc każdorazowo wzdłuż wytyczanej linii mocną kratę. Powierzchnia kolejno otrzymywanych części dąży do zera, tak że lew w końcu zostaje otoczony kratą o dowolnie małym parametrze.

Zauważmy, że zwięzłość ciała lwa w każdym wypadku nie jest mniejsza niż zwięzłość toroidu. Przekształcamy pustynię w przestrzeń czterowymiarową. Zgodnie z Lehrbuch der Topologie (H. Seifert i W. Threfall, 1934), w przestrzeni tej możemy w sposób ciągły wykonać taką deformację, że po powrocie do przestrzeni trójwymiarowej lew okaże się związany w węzeł. W takim stanie będzie on bezsilny.

5. Metoda Cauchy'ego albo funkcjonalno-teoretyczna

Rozpatrzmy lwa jako funkcję analityczną  f(z)  i napiszmy całkę:

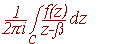
gdzie c, to krzywa ograniczająca pustynię (możemy po niej całkować bez obaw), a  ß  — punkt pustyni, w którym znajduje się klatka. Całka okazuje się po obliczeniu równa  f(ß) , tzn. lew jest w klatce.

Autor oryginalnego artykułu: G. Petard, profesor Uniwersytetu Princeton, NJ; z rosyjskiego (!) tłumaczenia tłumaczył na polski J. Knapik; skrócił A. Wrotniak)